A logic gate performs a logical operation on one or more logic inputs and produces a single logic output. The logic normally performed is Boolean logic and is most commonly found in digital circuits. Logic gates are primarily implemented electronically using diodes or transistors, but can also be constructed using electromagnetic relays, fluidics, optics, molecules, or even mechanical elements.
In electronic logic, a logic level is represented by a voltage or current, (which depends on the type of electronic logic in use). Each logic gate requires power so that it can source and sink currents to achieve the correct output voltage. In logic circuit diagrams the power is not shown, but in a full electronic schematic, power connections are required.
Truth table
A truth table is a table that describes the behaviour of a logic gate. It lists the value of the output for every possible combination of the inputs and can be used to simplify the number of logic gates and level of nesting in an electronic circuit. In general the truth table does not lead to an efficient implementation; a minimization procedure, using Karnaugh maps, the Quine–McCluskey algorithm or a heuristic algorithm is required for reducing the circuit complexity.
Logic gates
NAND and NOR logic gates are the two pillars of logic, in that all other types of Boolean logic gates (i.e., AND, OR, NOT, XOR, XNOR) can be created from a suitable network of just NAND or just NOR gate(s). They can be built from relays or transistors, or any other technology that can create an inverter and a two-input AND or OR gate. Hence the NAND and NOR gates are called the universal gates.
The four functions denoted by arrows are the logical implication functions. These functions are generally less common, and are usually not implemented directly as logic gates, but rather built out of gates like AND and OR.Symbols
There are two sets of symbols in common use, both now defined by ANSI/IEEE Std 91-1984 and its supplement ANSI/IEEE Std 91a-1991. The "distinctive shape" set, based on traditional schematics, is used for simple drawings and is quicker to draw by hand. It is sometimes unofficially described as "military", reflecting its origin if not its modern usage. The "rectangular shape" set, based on IEC 60617-12, has rectangular outlines for all types of gate, and allows representation of a much wider range of devices than is possible with the traditional symbols. The IEC's system has been adopted by other standards, such as EN 60617-12:1999 in Europe and BS EN 60617-12:1999 in the United Kingdom.
The goal of IEEE Std 91-1984 was to provide a uniform method of describing the complex logic functions of digital circuits with schematic symbols. These functions were more complex than simple AND and OR gates. They could be medium scale circuits such as a 4-bit counter to a large scale circuits such as a microprocessor. The 1984 version did not include the "distinctive shape" symbols.[1] These were added to the 1991 supplement with this note: "The distinctive-shape symbol is, according to IEC Publication 617, Part 12, not preferred, but is not considered to be in contradiction to that standard."
In the 1980s, schematics were the predominant method to design both circuit boards and custom ICs known as gate arrays. Today custom ICs and the field-programmable gate array are typically designed with Hardware Description Languages (HDL) such as Verilog or VHDL. The need for complex logic symbols has diminished and distinctive shape symbols are still the predominate style.
| Type | Distinctive shape | Rectangular shape | Boolean algebra between A & B | Truth table | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AND | 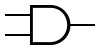 |  |  |
| ||||||||||||||||||
| OR |  | 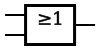 | A + B |
| ||||||||||||||||||
| NOT | 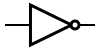 | 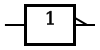 |  |
| ||||||||||||||||||
| In electronics a NOT gate is more commonly called an inverter. The circle on the symbol is called a bubble, and is generally used in circuit diagrams to indicate an inverted (active-low) input or output.[1] | ||||||||||||||||||||||
| NAND |  |  | 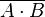 |
| ||||||||||||||||||
| NOR |  |  |  |
| ||||||||||||||||||
| XOR | 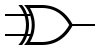 |  | 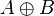 |
| ||||||||||||||||||
| XNOR | 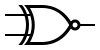 |  |  |
| ||||||||||||||||||
In practice, the cheapest gate to manufacture is usually the NAND gate. Additionally, Charles Sanders Peirce (1880) showed that NAND gates alone (as well as NOR gates alone) can be used to reproduce the functions of all the other logic gates, but his work on it was unpublished until 1935. The first published proof was by Henry M. Sheffer in 1913.
Two more gates are the exclusive-OR or XOR function and its inverse, exclusive-NOR or XNOR. The two input Exclusive-OR is true only when the two input values are different, false if they are equal, regardless of the value. If there are more than two inputs, the gate generates a true at its output if the number of trues at its input is odd ([2]). In practice, these gates are built from combinations of simpler logic gates.



No comments:
Post a Comment